Exercices de révision
Exercice 1
Écrivez le nomnbre suivant en notation scientifique : 0.0010112
Exercice 2
Convertissez en décimal le nombre binaire suivant : 101.10100112
Exercice 3
Convertissez en binaire le nombre décimal suivant : 27.421875
Exercice 4
Donner la représentation sur 32 bits du nombre suivant : 246.77734375
Exercice 5
Donner la valeur décimale de cette représentation sur 32 bits : 1 10011011 11010011011011011010000
Exercice 6
Donner l'expression logique de s :
| a | b | s |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Exercice 7
Donner l'expression logique de la sortie du schéma suivant :
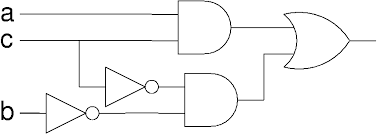
Exercice 8
Simplifiez l'expression logique suivante : a.(a + b + a) + b
