Booléens

Introduction
L’algèbre de Boole fut créé par George Boole au 19e siècle. Il permet de traduire des expressions logiques en opérations algébriques. Avec les travaux de Shannon et Turing, l’algèbre de Boole permettra la naissance de l’informatique.
Dans cette algèbre, il n’y a que 2 éléments : 0 ou 1 (faux ou vrai).
Un booléen est un type de variable qui peut prendre 2 états : 0 (pour faux) ou 1 (pour vrai).
En Python une variable sera un booléen si on lui attribue la valeur True (pour vrai) ou False (pour faux).
Opérateurs de base
Non
C’est l’opérateur de négation, il donne la valeur complémentaire du booléen. On notera le complémentaire de a : non(a), not(a) ou a (on dira alors « a barre » ou « non a »).
Pour expliciter un opérateur ou une fonction logique, on utilisera une table de vérité.
1) Complétons celle du non :
| a | a |
|---|---|
| 0 | |
| 1 |
| a | a |
|---|---|
| 0 | 1 |
| 1 | 0 |
En Python l’opérateur non s’écrit not.
2) Vérifions en Python l’opérateur not en saisissant les instructions suivantes :
>>> a = False
>>> not a>>> a = True
>>> not a>>> a = False
>>> not a
TrueEt
On le notera « . ».
3) Complétez alors sa table de vérité :
| a | b | a.b |
|---|---|---|
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
| a | b | a.b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
En Python l’opérateur et se note and.
4) Vérifions en Python l’opérateur and :
>>> True and False>>> False and False>>> True and True>>> True and False
False
>>> False and False
False
>>> True and True
TrueOu
On le notera « + ».
5) Complétez alors sa table de vérité :
| a | b | a + b |
|---|---|---|
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
| a | b | a + b |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
En Python l’opérateur ou se note or.
6) Vérifions en Python l’opérateur or :
>>> True or False>>> False or False>>> True or True>>> True or False
True
>>> False or False
False
>>> True or True
TrueLois de l’algèbre de Boole
Ces lois permettent de faire des calculs et simplifications à partir d'expressions booléennes. Nous utiliserons peu ces lois en première, mais il est important de connaitre leur existence.
Priorité
Le et est prioritaire sur le ou : a.b + c = (a.b) + c
Commutativité
L’ordre n’a pas d’importance : a + b = b + a ; a.b = b.a
Distributivité
On peut distribuer le et ainsi que le ou (cela est extrèmement contre-intuitif !) :
- a.(b + c) = a.b + a.c (distributivité de « . »)
- a + (b.c) = (a + b).(a + c) (distributivité de « + »)
Idempotence
7) En complétant les tables de vérité suivantes, simplifier les expressions logiques « a.a » et « a + a »:
| a | a | a.a |
|---|---|---|
| 0 | 0 | |
| 1 | 1 |
| a | a | a + a |
|---|---|---|
| 0 | 0 | |
| 1 | 1 |
| a | a | a.a |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| a | a | a + a |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
et donc a.a = a et a + a = a.
Règles de De Morgan
8) Compléter les tables de vérité suivantes et en déduire une relation logique :
| a | b | a.b | a.b |
|---|---|---|---|
| 0 | 0 | ||
| 0 | 1 | ||
| 1 | 0 | ||
| 1 | 1 |
| a | a | b | b | a + b |
|---|---|---|---|---|
| 0 | 0 | |||
| 0 | 1 | |||
| 1 | 0 | |||
| 1 | 1 |
| a | b | a.b | a.b |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| a | a | b | b | a + b |
|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
et donc a.b = a + b
9) Compléter les tables de vérité suivantes et en déduire une relation logique :
| a | b | a + b | a + b |
|---|---|---|---|
| 0 | 0 | ||
| 0 | 1 | ||
| 1 | 0 | ||
| 1 | 1 |
| a | a | b | b | a.b |
|---|---|---|---|---|
| 0 | 0 | |||
| 0 | 1 | |||
| 1 | 0 | |||
| 1 | 1 |
| a | b | a + b | a + b |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
| a | a | b | b | a.b |
|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
et donc a + b = a.b
Fonctions composées
Toute expression logique peut s’écrire à partir des trois opérateurs de base mais pour simplifier les notations, il existe des fonctions composées.
Non et
On la note aussi nand : a nand b = a.b
Non ou
On la note aussi nor : a nor b = a + b
Ou exclusif
On le note aussi xor : a xor b = a.b + a.b
10) Compléter la table de vérité ci-dessous pour comprendre ce que fait un ou exclusif :
| a | b | a | b | a.b | a.b | a.b + a.b |
|---|---|---|---|---|---|---|
| 0 | 0 | |||||
| 0 | 1 | |||||
| 1 | 0 | |||||
| 1 | 1 |
| a | b | a | b | a.b | a.b | a.b + a.b |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
Circuits logiques
On peut représenter toutes ces fonctions sous forme de circuits logiques qu’on relie par des fils :
11) Indiquer les états intermédiaires sur le schéma suivant :
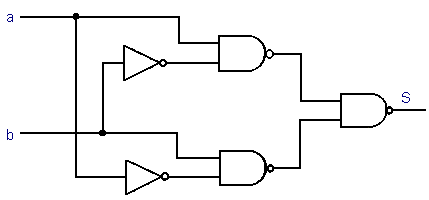
12) Simplifier l’expression de la sortie S en utilisant les règles de De Morgan.
Application à l’additionneur
13) Compléter la table de vérité d’un additionneur (addition de a et b) ci-dessous. s est la sortie et r la retenue.
| a | b | r | s |
|---|---|---|---|
| 0 | 0 | ||
| 0 | 1 | ||
| 1 | 0 | ||
| 1 | 1 |
14) Donner alors l’expression logique de s et r.
15) Représenter enfin cet additionneur sous la forme d’un circuit logique.
