Graphes et réseaux sociaux
Expérience de Milgram
En 1967, le psychosociologue Stanley Milgram effectua une expérience pour calculer les degrés de séparation entre deux personnes prises au hasard aux États-Unis.
1) Rechercher et décrire succinctement l’expérience de Milgram.
2) Suite à son expérience, Milgram en proposa d’expliquer ces résultats par le terme : « phénomène du petit monde ». Expliquer ce terme.
3) En 2011 Facebook calcula sur sa base de donnée le degré de séparation moyen entre deux personnes. Quel fut le résultat ?
Graphe social
Description en texte
On peut décrire un réseau social avec des phrases :
- Tom est ami avec Emma, Claire et Mattéo ;
- Claire est amie avec Tom, Emma et David ;
- Mattéo est ami avec Tom et Kevin ;
- Emma est amie avec Tom et Claire ;
- David est ami avec Claire ;
- Kevin est ami avec Mattéo.
Cette description n’est pas très pratique car elle ne permet pas de voir rapidement les liens entre les personnes. On utilisera d’autres représentations.
Description en tableau
En informatique, on pourra utiliser un tableau pour décrire un réseau social. Ce sera un tableau à double entrée avec une case cochée lorsqu’il y a un lien entre deux personnes.
4) Complétez le tableau ci-dessous pour représenter le graphe social décrit plus haut.
| Tom | Claire | Mattéo | Emma | David | Kevin | |
| Tom | ||||||
| Claire | ||||||
| Mattéo | ||||||
| Emma | ||||||
| David | ||||||
| Kevin |
Description en graphe
La représentation la plus simple d’un réseau pour un humain est un graphe. Un graphe est un objet mathématique très simple avec lequel on peut faire des choses extrêmement compliquées. Il est constitué de sommets (ou nœuds) relié par des arêtes (ou liens). Si les arêtes sont fléchées, on parle de graphe orienté sinon on parle de graphe non-orienté.
5) Par quel type de graphe représente-t-on des liens d’amitié ?
6) Quel serait le type de graphe utilisé pour Twitter ou Instagram ?
7) Complétez le graphe ci-dessous pour représenter le graphe social décrit plus haut.
Propriétés des graphes
On peut trouver des centaines de propriétés et caractéristiques à un graphe, nous verrons seulement les plus utiles pour les graphes sociaux.
Une chaîne est une suite de sommets reliés par des arêtes dans un graphe non-orienté.
La longueur d’une chaîne est les nombre d’arêtes qui la compose.
La distance entre deux sommets est la longueur de la plus petite chaîne qui les relie.
8) Quelle est la distance entre :
- Tom et Emma ;
- David et Kevin ;
- Claire et Mattéo.
Le diamètre d’un graphe est la distance maximale entre deux sommets d’un graphe.
9) Complétez le tableau ci-dessous avec les distances entre chaque sommet.
| Tom | Claire | Mattéo | Emma | David | Kevin | |
| Tom | ||||||
| Claire | ||||||
| Mattéo | ||||||
| Emma | ||||||
| David | ||||||
| Kevin |
10) Déduire du tableau précédent le diamètre de ce graphe.
L’excentricité d’un sommet est sa distance maximale avec les autres sommets.
11) Complétez le tableau ci-dessous.
| Tom | Claire | Mattéo | Emma | David | Kevin | |
| Excentricité |
Le centre d’un graphe est l’ensemble des sommets avec l’excentricité minimale.
12) Déterminer le centre du graphe précédent.
13) Que peut-on remarquer à propos des sommets du centre du graphe ?
Le rayon d’un graphe est l’excentricité d’un des sommets du centre du graphe.
14) Déterminez le rayon du graphe précédent.
15) Déterminer le diamètre, le centre et le rayon du graphe ci-dessous.
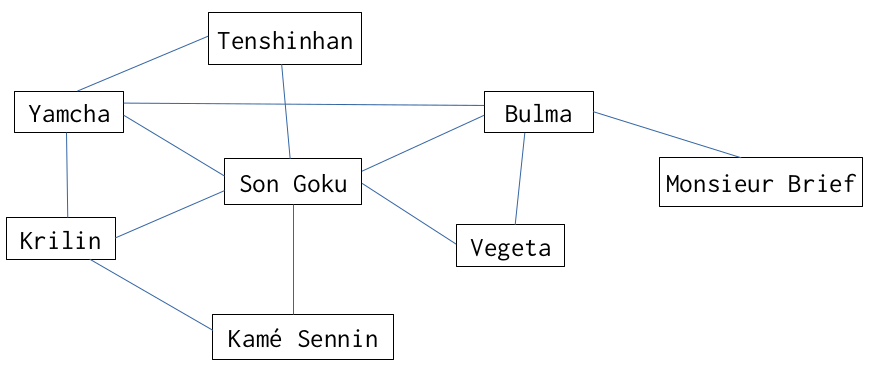
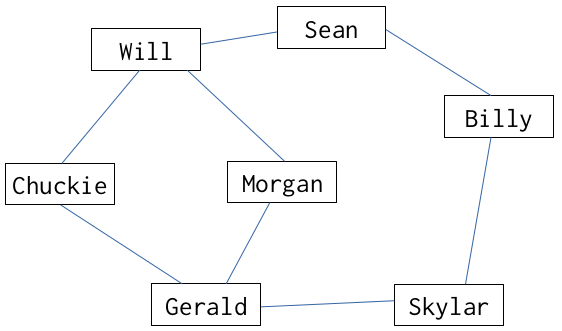
16) Déterminer le diamètre, le centre et le rayon du graphe ci-dessous.
17) [Bonus] Dans Will Hunting, le problème résolu par Will au tableau est un problème de graphe. Il faut trouver tous les arbres homéomorphiquement irréductibles de 10 sommets. Cela veut dire : un graphe de 10 sommets sans cycle (boucle) dont un sommet ne peut pas être relié à uniquement 2 autres sommets (1, 3, 4… mais pas 2). Essayez de résoudre ce problème.
