Exercices

Exercice 1

On cherche à calculer la somme des entiers de 1 à n avec une fonction somme(n).

1. Écrivez une fonction avec la méthode itérative permettant de répondre au problème.
2. Écrivez une fonction récursive permettant de répondre au problème.
3. Écrivez une fonction permettant de calculer directement le résultat sans boucle ni récursion.
4. Faites le bilan de l'occupation mémoire et du nombre d'opérations pour chacune des trois méthodes précédentes.

# 1.
def somme(n):
    s = 0
    for i in range(1, n + 1):
        s = s + i
    return s

# 2.
def somme_r(n):
    if n == 1:
        return 1
    else:
        return n + somme_r(n - 1)

# 3.
def somme_m(n):
    return n * (n + 1) / 2

Exercice 2

On cherche à calculer la somme des éléments d'une liste (un tableau).

1. Écrivez une fonction avec la méthode itérative permettant de répondre au problème.
2. Écrivez une fonction récursive permettant de répondre au problème. On rappelle que le premier élément d'une liste L se note L[0] et que le reste de la liste se note L[1:].

# 1.
def somme(L):
    s = 0
    for i in range(len(L)):
        s = s + L[i]
    return s

# 2.
def somme_r(L):
    if len(L) == 1:
        return L[0]
    else:
        return L[0] + somme_r(L[1:])

Exercice 3

Ici, on veut savoir si une chaîne de caractère est un palindrome, c'est à dire lue indifféremment de la gauche vers la droite et de la droite vers la gauche.

1. Écrivez une fonction récursive permettant de répondre au problème. On notera qu'on accède au premier élément d'une chaîne s avec s[0] et au dernier avec s[-1]. La chaine amputée de ses deux caractères extrème se note s[1:-1].
2. Décrivez le fonctionnement de votre programme avec le mot « snobons ».

# 1.
def palindrome(s):
    if len(s) == 0 or len(s) == 1:
        return True
    elif s[0] == s[-1]:
        return palindrome(s[1:-1])
    else:
        return False

Exercice 4

1. En partant du coin supérieur gauche, dessinez sur une feuille la figure suivante sans lever le stylo et sans repasser deux fois sur le même trait :

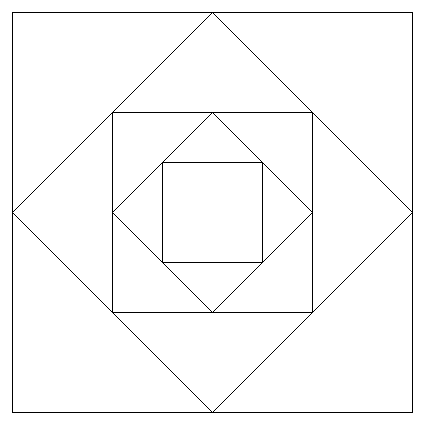
2. Proposez une fonction récursive à deux paramètres (la longueur du plus grand carré, le nombre de carrés imbriqués) permettant de réaliser ce dessin avec le module turtle.

from turtle import *
import math

speed(1) # On ralentit la tortue

def carres(longueur, nombre):
    forward(longueur)
    right(90)
    forward(longueur)
    right(90)
    forward(longueur)
    right(90)
    forward(longueur/2)
    if nombre > 1:
        right(45)
        carres(longueur / math.sqrt(2), nombre - 1)
    forward(longueur/2)
    right(45)

carres(400,5)

Exercice 5

Nous allons dessiner le fractal de Von Koch avec le module turtle. Nous allons avoir besoin de la récursivité. Nous dessinerons ensuite le flocon de Von Koch.

1. Créez une fonction récursive qui permet de dessiner le fractal de Kosh ci-dessous. La fonction de Koch prendra comme argument la longueur du segment et l'ordre : kosh(l,n)

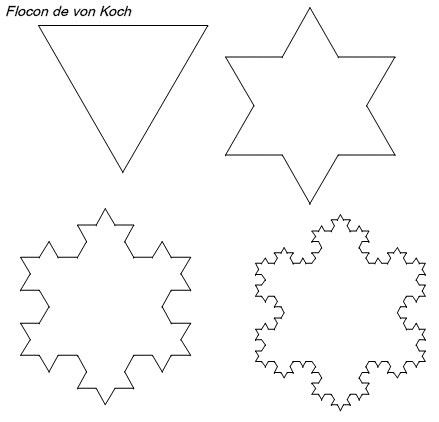
2. Créez une fonction (non récursive) utilisant la fonction de Kosh qui permet de dessiner le flocon de Kosh ci-dessous. Sont dessinés ci-dessous les flocons d'ordre 0, 1, 2 et 3. Cette fonction aura comme arguments la longueur du segment et l'ordre : flocon(l,n)

from turtle import *

ht() # On cache la tortue
speed(0) # Vitesse maximale

def koch(l,n):
    """Fractacle de Koch"""
    if n<=0:
        forward(l)
    else:
        koch(l/3,n-1)
        left(60)
        koch(l/3,n-1)
        right(120)
        koch(l/3,n-1)
        left(60)
        koch(l/3,n-1)

def flocon(l,n):
    """Flocon de Koch"""
    koch(l,n)
    right(120)
    koch(l,n)
    right(120)
    koch(l,n)

flocon(300,4)

Exercice 6

Nous considérons ici le quotient et le reste de la division euclidienne de n par d.

1. Écrivez une fonction récursive donnant le quotient de la division euclidienne de n par d sachant que ce quotient est le même que celui de (n -d) par d, plus 1. Faites attention au cas de base.
2. Écrivez une fonction récursive donnant le reste de la division euclidienne de n par d sachant que ce reste est le même que celui de (n - d) par d.